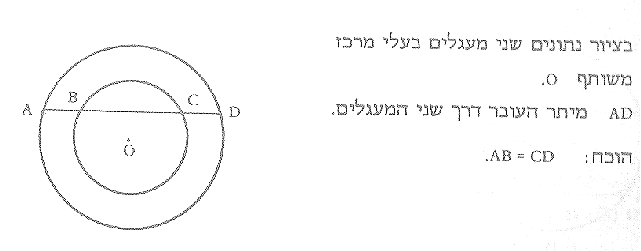
עבודה להגשה בהנדסת המישור. מעגל (לא כולל דימיון משולשים במעגל)

1.

רמזים:

א' משולש BOC הוא שווה שוקיים, זוויות OBC ו- OCB שוות. בהתאמה זוויות ABO ו- DCO שוות.

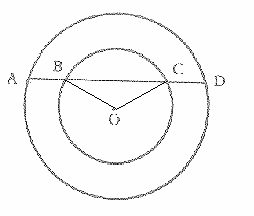
ב' משולש AOD הוא שווה שוקיים. זוויות BAO ו- CDO שוות.

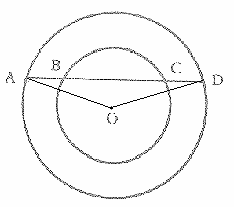
ג' במשולשים AOB ו- DOC יש שתי זוויות שוות בהתאמה – אז זוויות AOB ו- COD שוות.

משולשים AOB ו- DOC חופפים (צז"צ).

2.

רמזים:

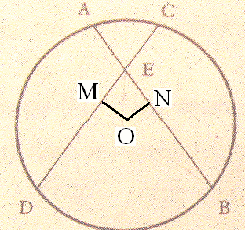
א' נסמן: M-אמצע של CD, ו- N-אמצע של AB. מקבלים: ON=OM (למה?). זוויות M ו-N ישרות (למה?)

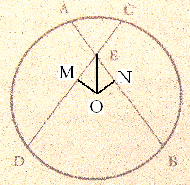
ב' משולשים MEO ו- NEO חופפים (צצ"ז). אז ME=NE.

3.

רמזים:

א' מיתרים שווים מרוחקים ממרכז המעגל במרחקים שווים. OH = OG.

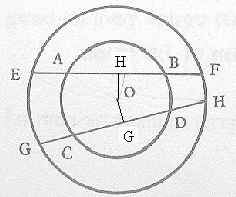
ב' משולשים AOH, BOH, COG ו- DOG חופפים (לפי ניתב ויתר).

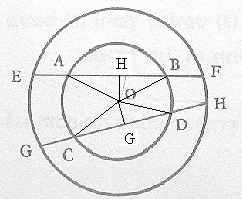
4.

רמזים:

א' נסמן: M – אמצע של EF (בהתאמה גם אמצע של KN).

OM – מאונך ל- EF. הוא גובה וגם תיכון במשולש KNO. אז KNO הוא משו"ש.

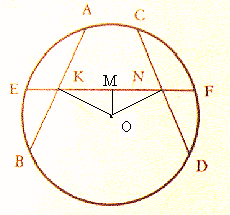
ב' מרחקים ממרכז המעגל למיתרים AB ו- CD שווים. אז המיתרים שווים.

5.

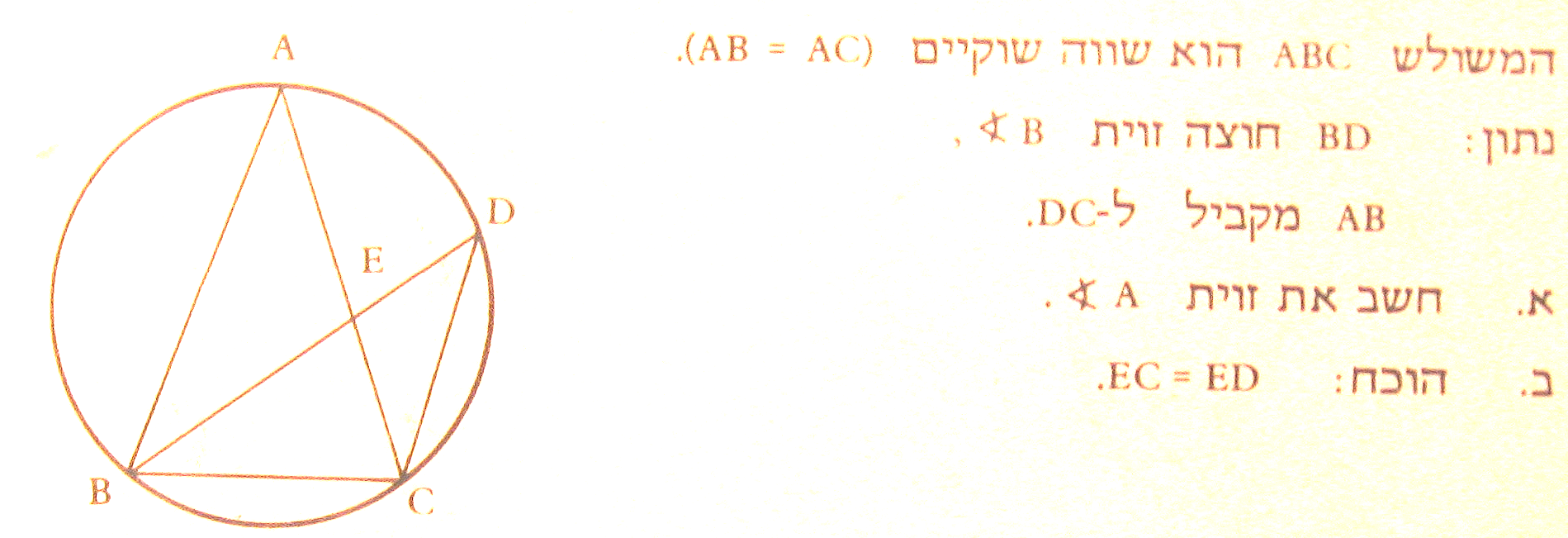
רמזים.

נסמן ב-X את זווית A. זווית D גם שווה ל-X (נשענת על אותה הקשת BC).

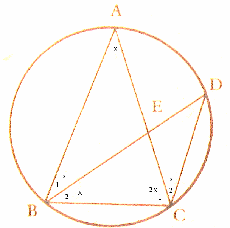
זווית B₁ גם שווה ל-X (מתחלפת עם זווית D).

זווית B₂ גם שווה ל-X (מפני ש- BD הוא חוצה זווית).

זווית C₂ גם שווה ל-X (נשענת יחד עם B1 על קשת AD.

זווית C₁ שווה לזווית ABC ושווה ל-2X.

סכום זוויות במשולש ABC שווה 180 מעלות.

6.

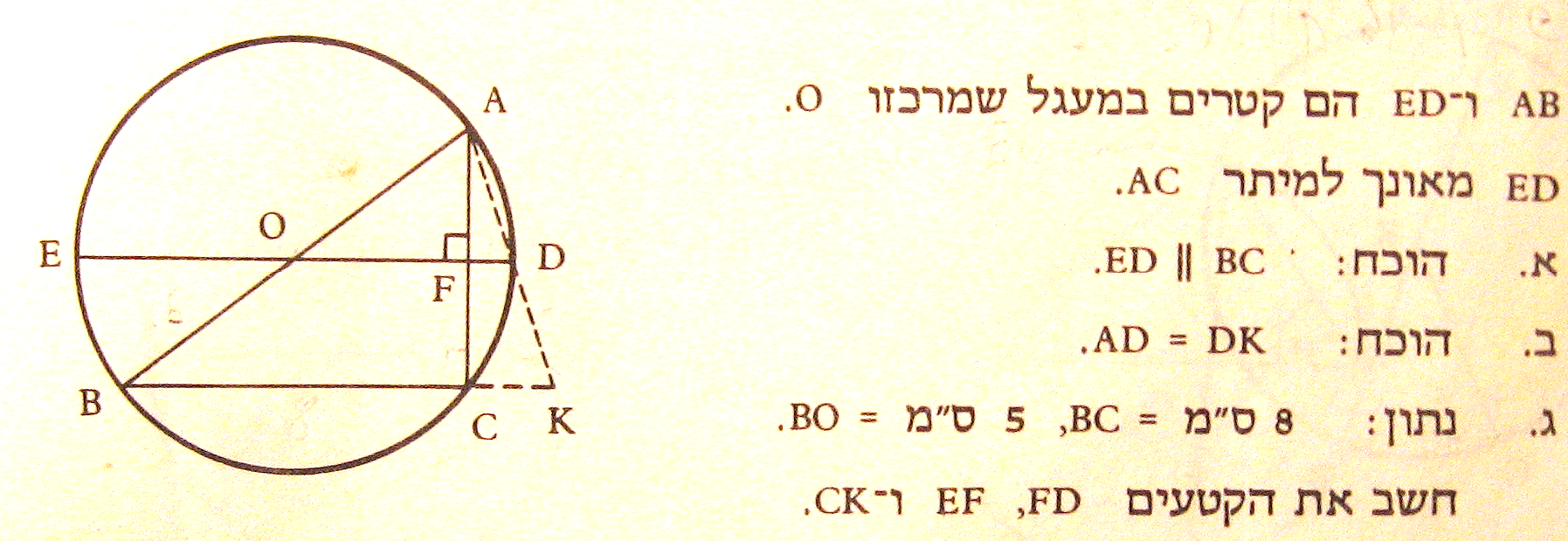
רמזים:

זווית C היא ישרה (נשענת על קוטר), זוויות C ו- F – מתאמות.

BO = OA = OE = OD ושווים לרדיוס המעגל (5 ס"מ).

במשולש BAC קטע OF עובר דרך אמצע צלע AB ומקביל לצלע BC , אז הוא – קטע אמצעים ושווה למחצית צלע BC.

OF = 4, OD=5, אז FD =1.

FD הוא קטע אמצעים במשולש CAK, אז הוא שווה למחצית צלע CK.

7.

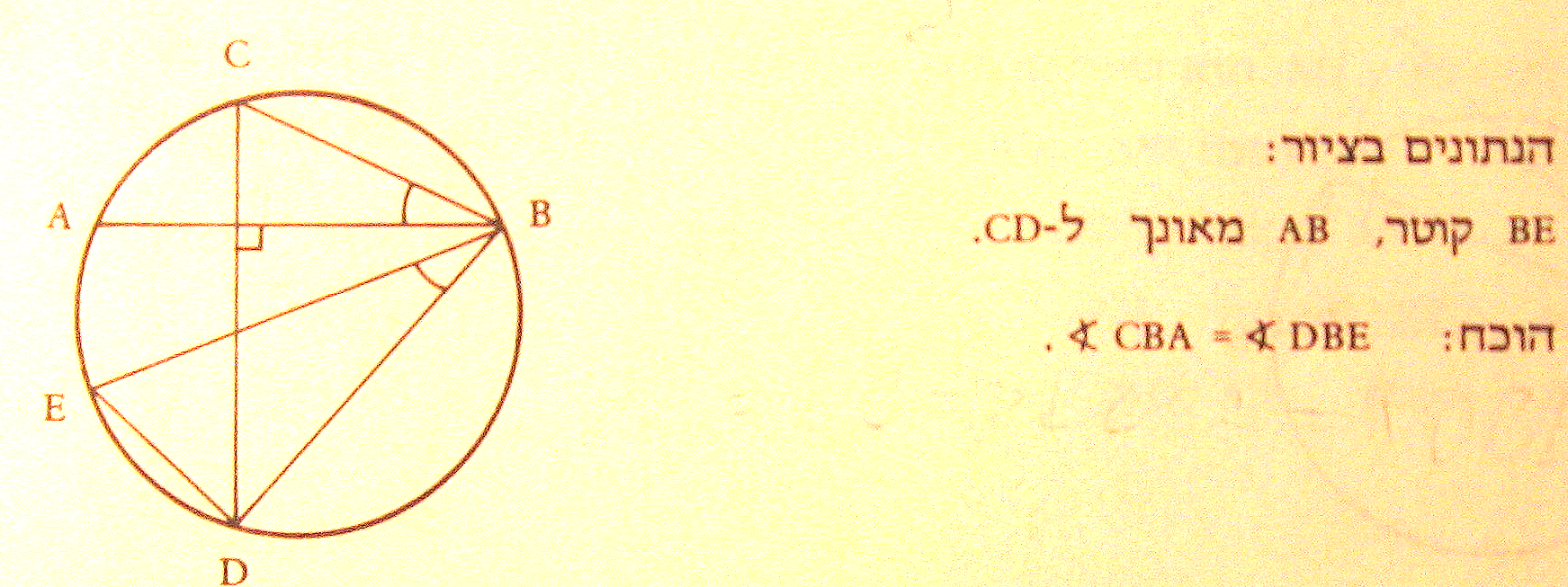
רמזים:

זוויות E ו- C שוות (נשענות על קשת BD). נסמן אותן ב-X.

נסמן ב-K את נקודת החיתוך של CD ו- AB.

זווית EDB ישרה (נשענת על קוטר).

זווית B במשולש CKB וזווית B שבמשולש EKB משלימות את X עד 90 מעלות.

8.

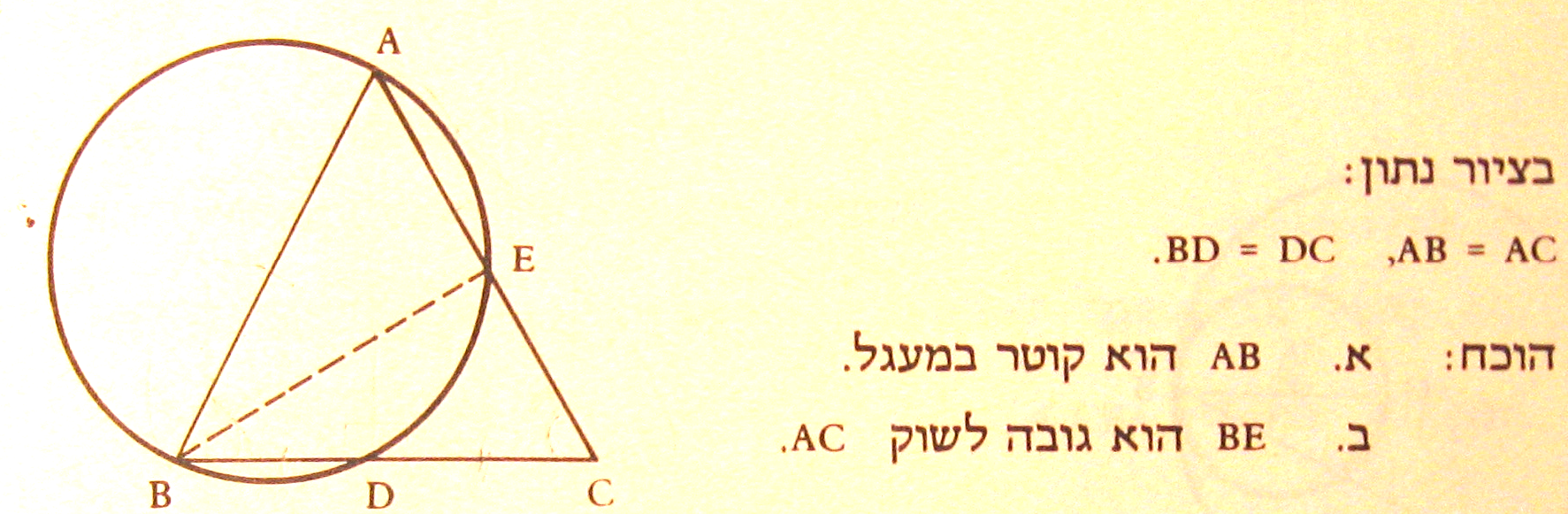
רמזים:

AD- הוא תיכון במושולש שווה שוקיים, אז הוא גם גובה. זווית D היא ישרה.

זווית ADB היא ישרה והיקפית, אז היא נשענת על הקוטר.

זווית AEB היא גם היקפית שנשענת על הקוטר.

9.

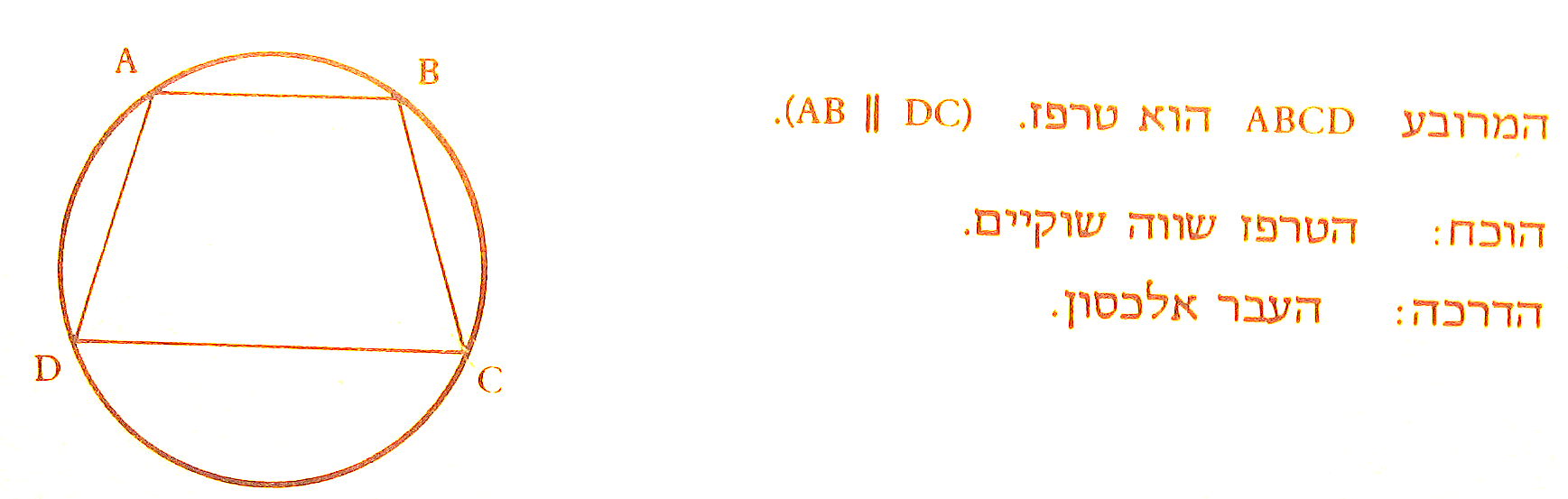
רמז:

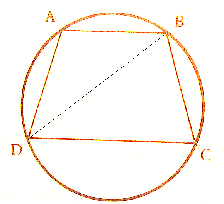
זוויות ABD ו- BDC שוות (כמתחלפות), אז הקשתות שעליהן הזוויות נשענות, גם שוות.

10.

רמזים:

א' במשולש EAB: קטע AC הוא גובה (כזווית ACB נשענת על הקוטר) וגם חוצה זווית.

אז משולש EAB הוא שווה שוקיים (AB=AE). בהתאמה, AC הוא גם תיכון (EC=CB).

ב' DC=CB (מיתרים, שעליהם נשענות זוויות שוות).

11.

רמז:

נעביר אלכסון BD. זוויות ADB ו- DBC נשענות על מיתרים שווים, אז הזוויות שוות.

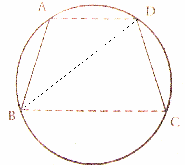
זוויות ADB ו- DBC הן זוויות מתחלפות ליד ישרים AD ו- BC.

12.

רמז: רדיוסים לנקודות ההשקה במעגל הקטן הם מרחקים ממרכז למיתרים במעגל הגדול.

13.

רמזים:

AE=AF=2 (משיקים מאותה הנקודה). AC=AB=5 (משו"ש). FB=EC=5-3=2.

DC=EC=2, וגם BF=BD=2.

14.

רמזים:

ED=EB, אז AE+ED=AE+EB=AB.

באותה הדרך מקבלים: AF+FD=AC.

אבל AB=AC.

15.

רמזים:

א' זווית A היא ישרה, אז DF הוא הקוטר. זווית E₁ גם נשענת על DF.

ב' זווית DEC (בין משיק למיתר) שווה לזווית DFE (היקפית שנשענת על אותו המיתר).

זוויות D₁ ו- D₂ משלימות אותן עד 90 מעלות במשולשים DEC ו- DFE בהתאמה.

16.

רמזים:

א' DA=DB (למה?), DA=DC(למה?).

ב' במשולש BAC תיכון לצלע שווה למחציתה.

17.

רמז:

MN הוא המשיק המשותף.

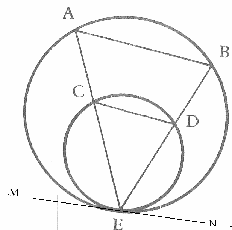
זווית MEC (בין משיק למיתר) שווה לזווית CDE (נשענת על מיתר CE במעגל הקטן) ושווה לזווית ABE (נשענת על מיתר AE במעגל הגדול). אז AB מקביל ל-CD (זוויות מתאמות שוות).

18.

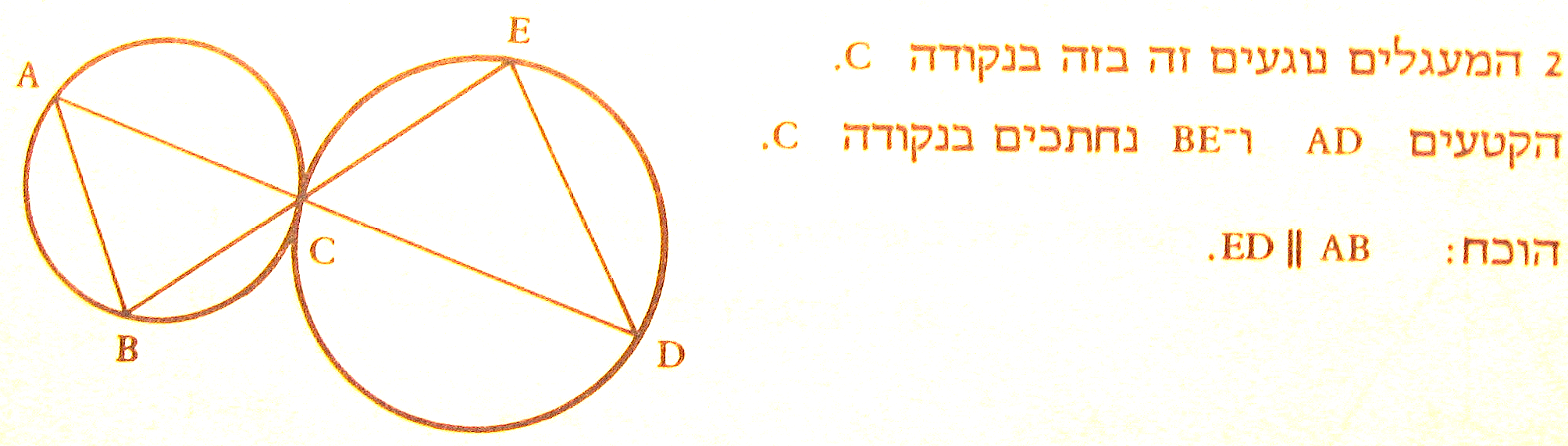
רמזים:

נעביר MN-משיק משותף.

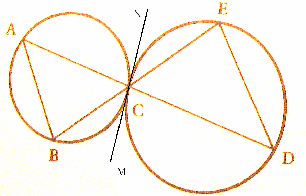
זוויות BCM ו- ECN שוות (כקודקודיות). זווית BCM (בין משיק למיתר) שווה לזווית BAC(נשענת על המעתר) וזווית ECN שווה בהתאמה לזווית EDC (למה?).

זוויות BAC ו- EDC – מתחלפות.

19.

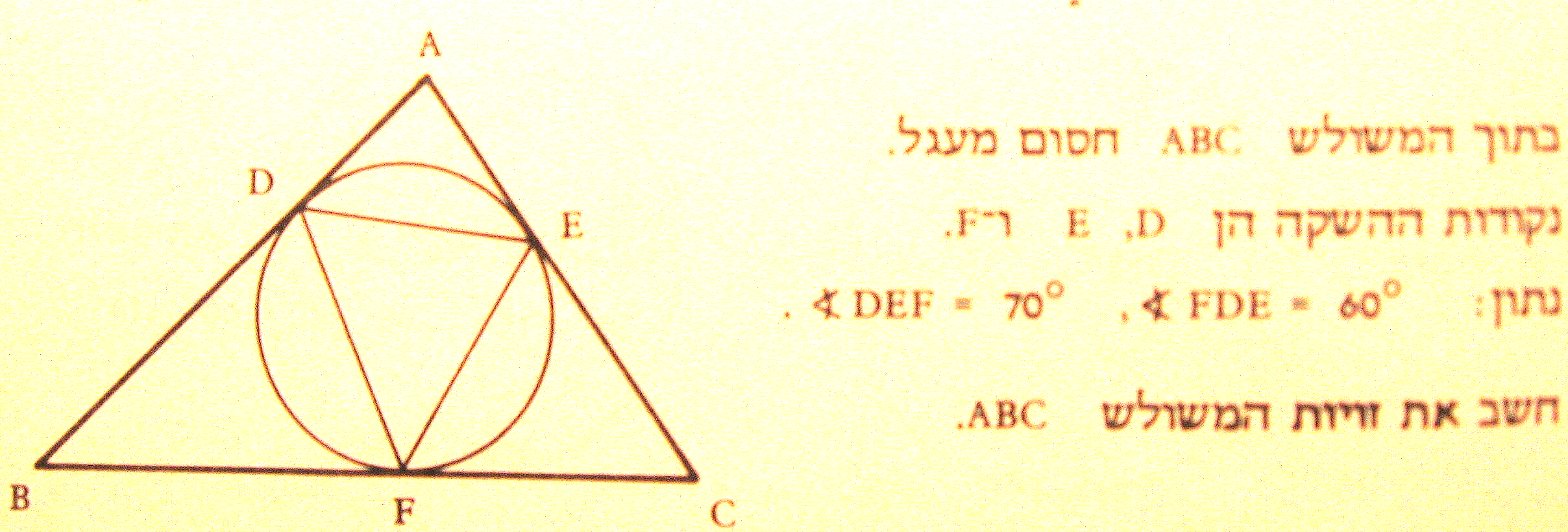
רמז. מה הקשר בין זווית בין שני משיקים לזווית המרכזית שנשענת על אותה המיתר?

20.

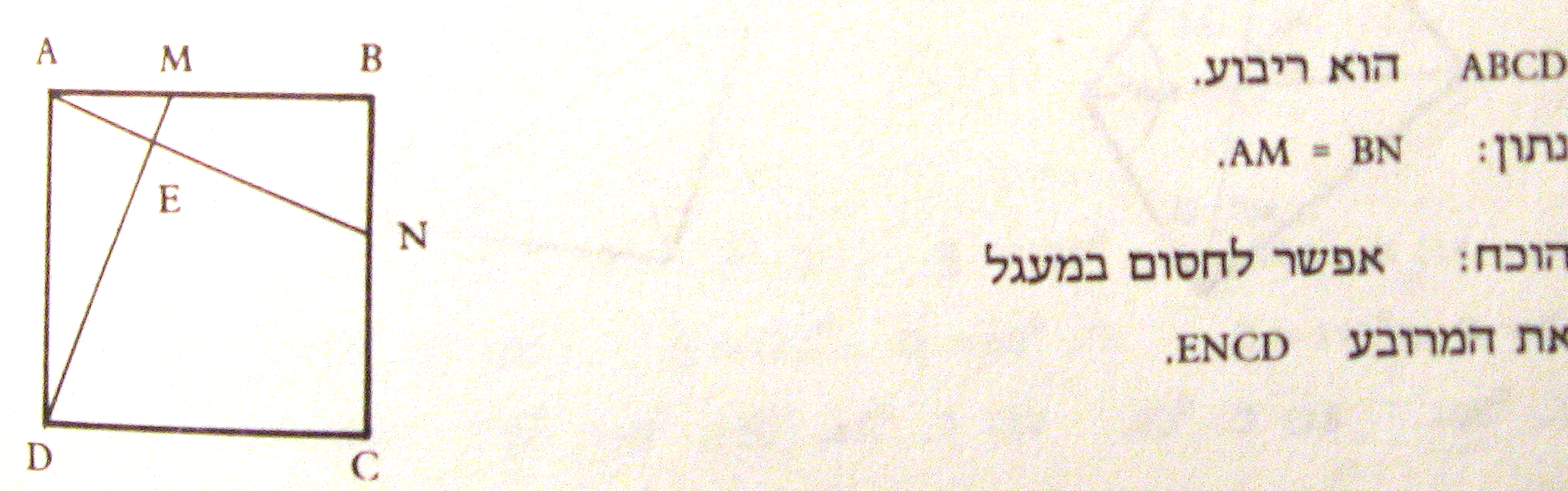
רמזים:

א' לחפוף משולשים ABN ו- DAM.

ב' לסמן את הזוויות BAN ו- ADM ב-X, בהתאמה זווית DAN משלימה את X עד 90 מעלות.

זווית E בת 90 מעלות (למה?).

ג' במרובע ENCD סכום זוויות E ו- C שווה ל-180 מעלות.

21.

רמזים:

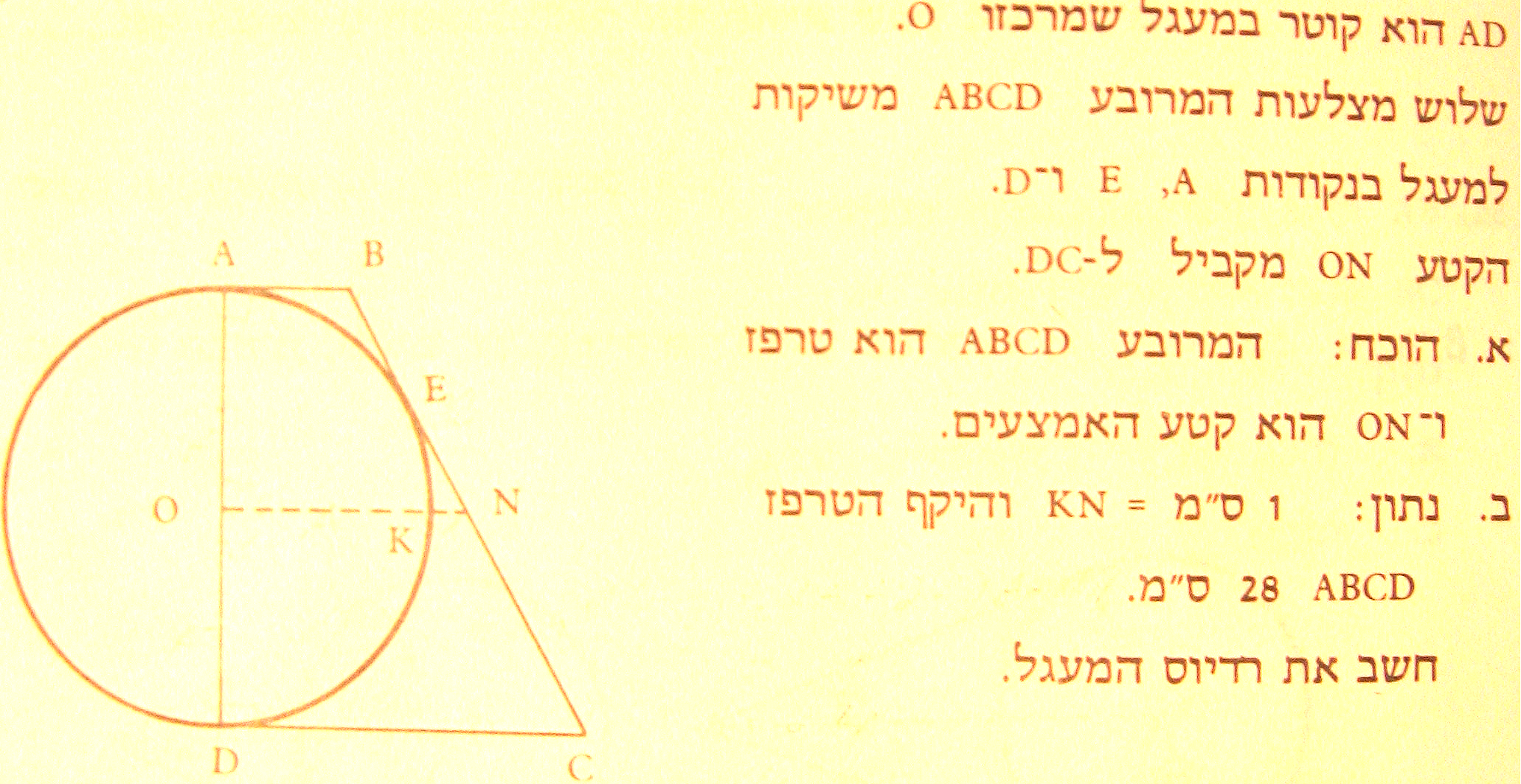
א' AB ו- DC שניהם מאונכים לקוטר AD, אז מקבילים אחד לשני.

ב' ON עובר דרך אמצע שוק אחת ומקביל לבסיסים – אז הוא קטע האמצעים.

ג' AB=BE (למה?), DC=EC(למה?). סכום הצלעות AB+BC+DC שווה לפעמיים BC.

ד' היקף הטרפז שווה לסכום של שני רדיוסים (קוטר AD) ושתי שוקיים BC. אז R+BC=14.

מצד שני,

ON=R+1=0.5(AB+DC)=0.5BC

אז BC=2R+2.

מקבלים:

R+2R+2=14.

משפטים:

1. לקשתות שוות מתאימים מיתרים שווים ולהפך.

2. אנך ממרכז למיתר חוצה את המיתר.

3. אנך אמצעי למיתר עובר דרך מרכז המעגל.

4. מיתרים שווים נמצאים במרחקים שווים ממרכז המעגל.

5. הזווית המרכזית גדולה פי 2 מכל זווית היקפית שנשענת על אותה הקשת.

6. זווית היקפית שנשענת על המיתר היא זווית ישרה.

7. זוויות היקפיות שוות נשענות על מיתרים שווים.

8. המשיק מאונך לרדיוס בנקודת ההשקה.

9. זווית בין משיק למיתר בנקודת ההשקה שווה לזווית היקפית שנשענת על אותו המיתר.

10. שני משיקים למעגל מאותה הנקודה שווים.

11. מרכז המעגל החוסם את המשולש – נקודת חיתוך של שלושה אנכים אמצעים לשלוש צלעות המשולש.

12. מרכז המעגל החסום במשולש – נקודת חיתוך של שלושה חוצי זוויות.

13. מרובע בר חסימה – סכום כל שתי זוויות נגדיות שווה ל- 180 מעלות, ולהפך.